DAX en 5D

Vamos a analizar en oeriodo de 5 D, no en semanal, pues vamos arrastrando las operaciones,

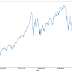
este seria el grafico en 1D y el grafico en 5D

Y estos son los datos de ROC1

otal aciertos 2251
total fallos   1902
total          4153
% aciertos     54
suma aciertos 23.0484912186
suma fallos   -19.4543900904
ratio 1.18474499131
total fallos   1902
sharpe         0.944223582916

<matplotlib.figure.Figure at 0x7f80c32831d0>

95% de no perder mas de
-0.0701156476022
Mediana de la distribucion, trata que sea positiva
0.0199882625362
media de la distribucion
0.0171131902314
maxima ganancia mensual
0.311658160412
maxima perdida mensual
-0.191017265144
desviacion tipica
0.0533079826385
dos veces la desviacion tipica
-0.0895027750455
tres veces la desviacion tipica
-0.142810757684

Y estos los de ROC5

total aciertos 2318
total fallos   1835
total          4153
% aciertos     55
suma aciertos 52.368841575
suma fallos   -43.3040282784
ratio 1.20932956256
total fallos   1835
sharpe         1.11638100334

<matplotlib.figure.Figure at 0x7f80c3239290>

95% de no perder mas de
-0.397773125263
Mediana de la distribucion, trata que sea positiva
0.0735622774365
media de la distribucion
0.0430925040377
maxima ganancia mensual
1.06782979212
maxima perdida mensual
-1.164335774
desviacion tipica
0.262964567145
dos veces la desviacion tipica
-0.482836630253
tres veces la desviacion tipica
-0.745801197398

Vemos que tienen unos ratios de sharpe parecidos, pero la alta volatilidad le afecta a ROC5 pues es como si hubieramos multiplcado por 5 ROC1.

para aplicar nuestros resultados desplazamo un periodo hacia atras nuestro ROC5

encontramos 3 arboles de decision y nos da los siguientes resultados

	resultado2	resultado3	resultado4	resultado4a	roc5
Date
2017-08-23	1	1	1	-0.010261	-0.007303
2017-08-24	1	1	1	-0.002079	-0.001854
2017-08-25	1	1	1	-0.001754	0.000226
2017-08-28	1	1	1	0.014886	0.004764
2017-08-29	1	1	1	0.017669	-0.023179
2017-08-30	1	1	1	0.019973	-0.014114
2017-08-31	1	1	1	0.013287	-0.010261
2017-09-01	0	1	1	0.000000	-0.002079
2017-09-04	1	1	1	0.033081	-0.001754
2017-09-05	1	1	1	0.027756	0.014886
2017-09-06	0	1	1	0.000000	0.017669
2017-09-07	0	1	1	0.000000	0.019973
2017-09-08	0	1	1	0.000000	0.013287
2017-09-11	0	1	1	0.000000	0.030823
2017-09-12	0	1	1	0.000000	0.033081
2017-09-13	0	1	1	0.000000	0.027756
2017-09-14	1	1	1	0.000000	0.019828
2017-09-15	1	1	1	0.000000	0.017460
2017-09-18	1	1	1	0.000000	0.006745
2017-09-19	1	1	1	0.000000	0.000800

Sólo entraremos cuando tenemos tres unos, por ejemplo, tenemos 4 operaciones abiertas y parece que con un buen rumbo.

total aciertos 1283
total fallos   915
total          2198
% aciertos     58
suma aciertos 26.5523307672
suma fallos   -18.2080091063
ratio 1.45827754216
total fallos   915
sharpe         1.70780588179

<matplotlib.figure.Figure at 0x7f80c3397410>

95% de no perder mas de
-0.234417613914
Mediana de la distribucion, trata que sea positiva
0.0375934480488
media de la distribucion
0.0401124396769
maxima ganancia mensual
0.601535815741
maxima perdida mensual
-0.404273922434
desviacion tipica
0.147272833439
dos veces la desviacion tipica
-0.2544332272
tres veces la desviacion tipica
-0.401706060639

y esta tabla menusual de resultados

Month	1	2	3	4	5	6	7	8	9	10	11	12	All
Year
2000	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	0.029401	-0.199037	-0.056109	-0.225745
2001	-0.015337	-0.278239	0.000000	0.039390	0.154319	-0.089747	-0.132493	-0.172211	0.000000	0.000000	0.183154	0.104501	-0.206663
2002	-0.284476	0.315031	-0.050930	-0.261608	-0.246437	0.000000	0.000000	0.000000	0.000000	0.000000	-0.075851	-0.070796	-0.675066
2003	-0.221124	0.000000	0.000000	0.225896	0.248789	0.300355	0.228768	0.272762	0.023557	0.452112	0.071363	0.000000	1.602477
2004	0.000000	0.063786	-0.209294	-0.061734	-0.011626	0.086556	-0.102504	-0.099726	0.202924	0.047288	0.081978	0.081198	0.078847
2005	0.042069	0.042200	0.004390	-0.041498	0.204630	0.035153	0.131189	0.108329	0.130534	-0.010067	0.170099	0.086177	0.903204
2006	0.154408	0.073741	0.170866	0.098604	-0.214064	-0.121344	-0.078097	0.169977	0.162976	0.111210	0.059042	0.134870	0.722189
2007	0.187596	-0.154280	0.278264	0.152601	0.148856	0.293957	-0.252756	0.053199	0.239084	-0.009063	0.020868	0.069305	1.027632
2008	-0.339935	0.000000	0.000000	0.067104	0.033421	-0.404274	0.044904	-0.100731	-0.016031	0.000000	0.000000	0.000000	-0.715543
2009	0.000000	0.000000	0.000000	0.371037	0.183133	-0.238539	0.443064	0.154516	0.128518	0.074242	0.227550	0.115525	1.459046
2010	-0.359526	0.289331	0.147759	-0.155499	0.164059	0.015460	0.344941	-0.008403	0.028620	0.221579	0.189976	-0.022142	0.856154
2011	0.179239	-0.018686	0.010461	0.168888	-0.227920	0.166585	0.055085	0.000000	0.000000	0.013371	-0.013763	0.207888	0.541148
2012	0.415858	0.061041	0.065655	-0.074021	-0.168936	0.000000	0.371307	0.154067	0.084643	0.073840	0.120802	0.038283	1.142540
2013	-0.037233	0.180999	-0.107051	0.162207	-0.062531	-0.135300	0.243270	-0.022214	0.088969	0.160207	0.104300	0.149354	0.724977
2014	-0.038278	0.084770	-0.032024	0.057134	0.190762	0.000436	-0.341870	0.116741	-0.214404	-0.014309	0.132900	-0.080982	-0.139124
2015	0.322181	0.142564	0.000000	0.020943	-0.000652	-0.077312	0.090454	-0.156905	0.000000	0.008406	0.043422	-0.251964	0.141137
2016	-0.153872	0.000000	-0.135340	0.033606	0.212222	-0.083992	0.210452	0.207667	-0.021111	0.115399	0.157345	0.207679	0.750056
2017	0.014322	0.113216	0.135369	0.138368	0.025037	-0.125751	0.003774	-0.008116	0.060837	NaN	NaN	NaN	0.357057
All	-0.134106	0.915474	0.278124	0.941417	0.633063	-0.377756	1.259487	0.668952	0.899115	1.273615	1.274149	0.712788	8.344322

Podemos comparar las dos series, inicial y final

95% de no perder mas de
-0.397773125263
95% de no perder mas de
-0.270402900251
95% de no perder mas de
-0.397773125263 -0.270402900251
Mediana de la distribucion, trata que sea positiva
0.0735622774365 0.08847237758
media de la distribucion
0.0430925040377 0.0770140705268
maxima ganancia mensual
1.06782979212 0.670358979577
maxima perdida mensual
-1.164335774 -0.523092347573
desviacion tipica
0.262964567145 0.202750944228
dos veces la desviacion tipica
-0.482836630253 -0.328487817929
tres veces la desviacion tipica
-0.745801197398 -0.531238762157
ratio sharpe anualizado
1.11638100334 1.70780588179